This page describes the various research areas we are working on.
For information on specific research projects go to the Projects page.

A main focus of our research is the understanding of the dynamics of human infectious diseases. We develop computational models, new analytic and numerical techniques and large-scale quantitative and predictive computer simulations to study various aspects of the dynamics of epidemics. In this research we combine mathematical methods from nonlinear dynamics, stochastic processes, statistical physics, complex network theory, and systems biology. We are interested in numerous aspects of disease dynamics, ranging from phenomena related to single populations to the large-scale spatial spread of epidemics.

Our research on computational epidemiology is funded in part by

• the Volkswagen Foundation within the program Complex Networks as a Phenomenon across Disciplines, and
• a Large-Scale Integrating Project (IP) within the Seventh Research Framework Programme (FP7) of the European Union: EPIWORK – Developing the framework for an epidemic forecast infrastructure.

We investigate to what extent human transportation networks and human mobility shape spatio-temporal disease dynamics. One of our goals is to determine and extract those statistical features of mobility networks that are most significant in determining typical (possibly universal) features of disease dynamics. This research is closely related to our projects on the structure of large- and multi-scale human mobility networks and to our research on fractional diffusion in heterogeneous environments.

See also The Origin of Wheresgeorge Research

In addition and in combination with models for the spatial spread of diseases we investigate the impact of social and behavioral heterogeneities on the time course of an epidemic in single populations. These differences could be seen in age-dependent transmission and recovery rates, pronounced variability in individual behavior, or, most importantly, in a broad distribution of contact rates. We are particularity interested in disease models that exhibit qualitatively new dynamics as a consequence of strong behavioral heterogeneities. To answer these questions we develop agent-based simulations in which each interacting unit is equipped with a set of individual parameters that are drawn from distributions that reflect the population’s heterogeneity.

Disease dynamics, the interplay of transmission and recovery in a population, are inherently stochastic processes, as individual events and interactions cannot be predicted. These stochastic effects are often ignored in mean-field models for disease dynamics. However, stochastic effects due to fluctuations dominate the time course of an epidemic, and in fact these effects are strongest at the epidemic’s onset. In a number of projects we aim to develop a systematic approach for incorporating stochastic effects into epidemic models. Of particular interest to us are emergent phenomena that arise in systems in which nonlinear dynamics, randomness, and spatial heterogeneity are combined, a condition typically met in epidemic contexts.

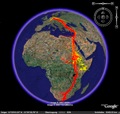
The phenomenon of human-mediated bioinvasion is conceptually related to the spatial spread of epidemics. Bioinvasion refers to the geographical expansion of a species into a new area in which they proliferate and persist to the detriment of the environment. Brought about largely through human transport and commerce, it is now recognized as one of the leading causes of the global biodiversity crisis. There is a great deal of evidence for the negative impact of alien invasive species on local species and habitats. Bioinvasion can lead to species extinction, loss of biodiversity, alteration of ecosystem function, and economic damage. A single introduced species can cause dramatic structural and functional changes: the introduction of the Nile perch to Lake Victoria brought about the extinction of over one hundred endemic fish species, the largest modern vertebrate extinction known. In collaboration with Bernd Blasius (ICBM, Oldenburg, Germany) and funded by the Volkswagen Foundation within the framework Complex Networks as a Phenomenon across Disciplines, we develop models for human-mediated bioinvasion processes on human transportation networks in order to quantify the susceptibility of various regions to bioinvasion threats and in order to develop more efficient containment strategies.

Projects:

• The Scaling Laws of Human Travel
• Influenza A(H1N1) Outbreak 2009 (Swine Flu)
• Impact of Social Heterogeneities in Epidemic Outbreaks
• Dynamics of Vaccination with Imperfect Knowledge
• Panic Reactions and Global Disease Dynamics
• Forecast and Control of Epidemics in a Globalized World

Publications:

1. L. Hufnagel, D. Brockmann and T. Geisel: Forecast and control of epidemics in a globalized world. Proc Natl Acad Sci USA 101, 15124 (2004). pdf
2. D. Brockmann, L. Hufnagel and T. Geisel: The scaling laws of human travel. Nature 439, 462 (2006). pdf
3. D. Brockmann: Human Mobility and Spatial Disease Dynamics. In Reviews of Nonlinear Dynamics and Complexity, H. G. Schuster (ed.), Wiley-VCH (2009). pdf

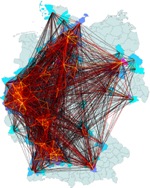
A key focus of our work is to reach a deeper understanding of complex biological and artificial networks. Particularly in connection to our research on spatial disease dynamics we are interested in the structure and properties of human mobility networks. Many of these networks can be described by a symmetric weight matrix whose elements are positive numbers that measure the flux of individuals between nodes. Transportation networks are usually strongly heterogeneous: the weights (traffic between nodes), capacities (total traffic through a node), and degrees (number of connections of a node) all exhibit very broad distributions. Unlike other complex networks such as author citation or gene regulatory networks, transportation networks are embedded in a metric space. This raises a number of interesting questions such as: How much of the embedding space is encoded in a transportation network? How do the statistical properties of a network depend on length scale? What are the differences between various transportation networks, and, more interestingly, what features do they share? Do nodes play different roles in a network based on their connectivity? How can these roles be characterized? What can transportation networks tell us about the connectivity of spatially distributed communities? Examples of networks we investigate are the worldwide air transportation network and multi-scale US and European networks, incorporating all means of transportation.

See also The Origin of Wheresgeorge Research

Projects:

• Community Structure in Multi-Scale Transportation Networks
• Beyond percolation theory: A local perspective of network resilience to real-world disasters
• Travel Bugs, Geocaching and European Traffic Networks
• The Scaling Laws of Human Travel
• Tour de Sys: The Traveler's View of a Network
• Universality in Multi-scale Transportation Networks

Publications:

1. D. Brockmann and F. Theis: Money Circulation, Trackable Items, and the Emergence of Universal Human Mobility Patterns. Pervasive Computing 7, Nr. 4, 28 (2008). pdf
2. L. Hufnagel, D. Brockmann and T. Geisel: Forecast and control of epidemics in a globalized world. Proc Natl Acad Sci USA 101, 15124 (2004). pdf
3. D. Brockmann, L. Hufnagel and T. Geisel: The scaling laws of human travel. Nature 439, 462 (2006). pdf
4. D. Brockmann: Anomalous diffusion and the structure of human transportation networks. European Physical Journal - Special Topics 157, 173-189 (2008). pdf

Complex dynamical phenomena in biological systems across many orders of magnitude in length scale are governed by the interplay of nonlinear interactions, structural inhomogeneities, randomness, and topological complexity of the internal interactions. Examples of such systems abound: gene regulatory systems, metabolic networks, intracellular transport, and entire ecosystems all share a surprising number of features. Despite their complexity and regardless of length scale, they are surprisingly robust with respect to external perturbations and flexible with respect to internal changes. Using methods from systems biology, nonlinear dynamics, and stochastic processes we investigate the dynamics of these biological systems in a number of case studies. In one focus area we model the facilitated target localization of transcription factors on DNA based on intersegment transfer due to the dynamic thermal folding of DNA. Along a more theoretical line of research we investigate particle reaction kinetics in regulatory networks, with a particular emphasis on the impact of stochasticity in combination with the complex coupling of the network.

Anomalous diffusion processes are random dispersal processes that exhibit a temporal scaling of position that is in conflict with the square root behavior of ordinary diffusion (Brownian motion). Processes that disperse faster are called superdiffusive, and those that disperse more slowly, subdiffusive. Our research on anomalous diffusion processes focuses mostly on anomalous diffusion processes when they evolve in structured environments or when they are subjected to spatially variable forces or potentials. We developed a theoretical framework employing fractional Fokker–Planck equations in which the anomalous diffusion in the face of spatial heterogeneities can be described consistently. A key prediction made by these models is that the combination of anomalous diffusion in a structured environment can exhibit surprising and counterintuitive behavior.

Publications:

1. D. Brockmann and L. Hufnagel: Front propagation in reaction-superdiffusion dynamics: Taming Levy flights with fluctuations. Phys Rev Lett 98, 178301 (2007). pdf
2. D. Brockmann and T. Geisel: Particle dispersion on rapidly folding random heteropolymers. Phys Rev Lett 91, 48303 (2003). pdf
3. D. Brockmann and T. Geisel: Levy flights in inhomogeneous media. Phys Rev Lett 90, 170601 (2003). pdf
4. D. Brockmann and I. M. Sokolov: Levy flights in external force fields: from models to equations. Chem Phys 284, 409 (2002). pdf