The Origin of Wheresgeorge Research
Dirk Brockmann, Northwestern University
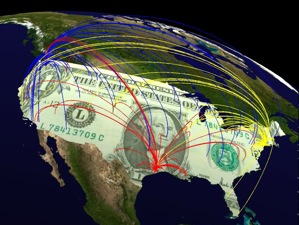
At that time I had just finished my dissertation on anomalous diffusion processes at the same institute. Lars approached me with his idea, seeking my expertise on diffusion processes and random walks. I found his ideas very interesting and challenging so we started working on a model for the worldwide spread of SARS. Initially I was very pessimistic, thinking that human infectious diseases and mobility patterns are so complex that the chances of predicting spreading patterns were very small. Yet to my surprise a key result of our SARS study was that global spreading patterns are indeed largely determined by the global mobility network.
Shortly after we published the paper on SARS, I realized that although our approach worked well on a global scale it was insufficient to account for the spread of epidemics on intermediate and shorter distances. Within a single country it could potentially yield wrong answers if one ignored traffic that occurs on shorter length scales: daily commuting traffic by car or local public transportation systems, and intermediate distance traffic by trains and other means of transportation. At that time I was thinking about ways to collect data on human mobility on all spatial scales all over the world in order to compile them into a comprehensive data set that would capture the characteristics of all possible means of human mobility. My goal was the construction of an international multi-scale mobility network, a task that I knew was very difficult at best, and impossible at worst.
Wrapped up in these thoughts I attended a physics conference in Montreal. After the conference I decided to visit Dennis Derryberry, an old friend from college who lives within driving distance to Montreal in the green mountains of Vermont, where he works as a cabinet maker. After a few hours on the highway Dennis and his family welcomed me to their beautiful house in the woods. During this visit Dennis, one of the most witty individuals I have ever met, asked me one evening on his porch while we were having a beer, “So Dirk, what are you working on?” – “I’m interested in the patterns that underly human travel,” I replied, and told him about my efforts to better understand human mobility and our goal of developing more quantitative models for the spread of epidemics. “It’s just amazingly difficult to compile all this data,” I explained. Dennis paused a while and then inquired, “Do you know this website www.wheresgeorge.com?”
I didn’t. But it was at this moment when it all started. I asked Dennis about the website and he told me it was some sort of online bill tracking system, but that evening on the porch I formed only a vague idea. The next morning he showed me the website and it became clear to me that, in a flash, it could solve a number of our most pressing problems. Wheresgeorge tracks the geographic circulation of individual dollar bills in the United States. Individual bills are marked by a large community of “Georgers” throughout the US. If any person gets hold of a marked bill and visits the website, they can provide their current zip code and the serial number of the bill. Once the bill is back in circulation it can be reported again at another time and place by some other person, thereby generating a trajectory of a bill throughout the country. For each registered bill one can monitor these movements and study the logs that individual finders post. Forming a mental image of millions of these dollar bill journeys in my head, I was convinced that analyzing this data would reveal essential properties of human mobility, the driving force behind the dispersal of bank notes. Dennis’ intellectual spark triggered a whole series of studies of human mobility based on this idea.
After my visit to Dennis’ house in Vermont I returned to Göttingen and immediately told Lars about wheresgeorge.com. We started discussing the possibility of using this data for our science and decided to contact Hank Eskin, the man behind wheresgeorge.com, to ask him if he could provide us with some of his data. We sent an email to Hank and for a few days we were impatiently awaiting his response. Meanwhile we studied the information that was available on the wheresgeorge.com website. It turned out that all the information we needed was already available on the website and all we lacked was an automated method for collecting it. While waiting for a response from Hank, Lars wrote a little program that systematically scraped bill reports from the website. Every morning in our office we checked the growing number of reports that we downloaded from wheresgeorge.com.
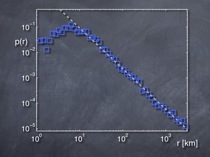
The probability p(r) of a dollar bill traversing a
distance r in a short period of time follows a simple
mathematical relation known as a power law. We computed
this from over a million trajectories of dollar bills
in the United States.
Meanwhile, Hank noted some systematic high frequency visits to his website generated by our program and discovered that someone from Germany was reading out data. We didn’t know this at the time and were surprised when one day we could no longer access wheresgeorge.com from the computers in our office. First we thought that it was a local network problem, but it wasn’t. As a precaution, Hank had denied access to whoever it was that was reading out the data. In fact, he was so cautious that he blocked access from the entire city of Göttingen. We were disappointed, of course, but realized that we had probably caused this access denial. However, we had already downloaded more than a million individual dollar bill trajectories, which was sufficient for our first analysis.
I decided the simplest and most straightforward quantity to compute for our initial investigation was the probability of a bill traveling a certain distance in, say, a day. I was actually quite pessimistic at first and didn’t expect to see any particular structure; imagine my excitement and surprise when instead I found that this probability follows a very simple mathematical law! Intuitively it is clear that long journeys of 1000 miles, for example, are less frequent than short ones of a few miles. Yet the particular way this probability decreases with distance turned out to obey a very simple relation, a so-called power law. From my work on anomalous diffusion I knew that this had some very fundamental implications: the dispersal of dollar bills is scale free, self-similar, and fractal. I was very excited to discover these simple mathematical laws underlying the movement of dollar bills, and it turned out that additional simple patterns concerning mobility were hidden in the data. We summarized these discoveries in a manuscript that was published in early 2006.2
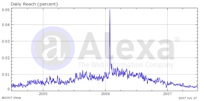
Daily reach traffic on www.wheresgeorge.com. The
central peak on Jan 24th, 2006 coincides with the
publication of The scaling laws of human
travel2. (Source: www.alexa.com)
This paper elicited an immediate response from the mainstream press, and shortly after publication Hank Eskin noted an unusual increase in the number of hits on his website. In fact he had to deal with an overload of requests to wheresgeorge.com and was also contacted by journalists who asked whether he had heard about the group of German scientists who used his data in their study of human mobility and disease spread. He quickly realized that it was those same Germans who had contacted him more than a year earlier. Hank, and very many Georgers, were excited that wheresgeorge.com had become the central piece in a study that, for the first time, mathematically analyzed human mobility from a few to a few thousand miles and that this website had lead to the discovery of the scaling laws of human mobility and promised to be key to improving models for pandemic disease forecast.
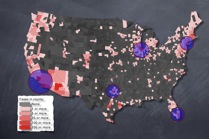
Based on wheresgeorge.com data, we estimated
multi-scale human mobility networks. These networks
were the foundation of our computational model for the
most likely time course of the spread of the H1N1
pandemic (swine flu) in the United States in early
2009.
After publication Hank contacted Lars, and ever since then we’ve been in close communication. Hank was kind enough to provide his entire data set for our research, which is now the core of more sophisticated projects. In fact, in April 2009 we used the Wheresgeorge data to model the spread of swine flu through the United States and computed projections of the time course of the spread. Without wheresgeorge.com these large scale computer simulations would not have been possible. We continue to study the structure of human mobility using bill tracking and are optimistic that more secrets will be revealed by this marvelous data set. We are deeply thankful to Hank Eskin for generously providing this data, the large community of Georgers that generated this data over the years, and finally to the cabinet maker and friend Dennis Derryberry, who that evening on the porch in Vermont had the right thought at the right moment.
(Ed.: Daniel Grady)
Download PDF of this page
Download PDF of this page
1 L. Hufnagel,
D. Brockmann and T. Geisel: Forecast
and control of epidemics in a globalized
world.
Proc Natl Acad Sci USA 101,
15124 (2004). ![]() pdf
pdf
2 D. Brockmann,
L. Hufnagel and T. Geisel: The scaling
laws of human travel.
Nature 439, 462 (2006).
![]() pdf
pdf