Dynamics of Vaccination with Imperfect Knowledge
A high enough vaccine coverage level can eradicate a disease from a population. However, if individuals believe there is any risk associated with the vaccine, vaccination decisions driven by rational self-interest can keep the overall vaccination below this level. If almost everyone in a population has chosen to vaccinate, an unvaccinated individual may believe that it's unlikely that they will come into contact with someone who is infected, and thus they will feel more comfortable choosing not to vaccinate. We investigate how the likelihood that a disease is eradicated from a population (and other features of system dynamics) change as the amount of inter-individual interaction and the amount of information each individual has about the world vary from local to global.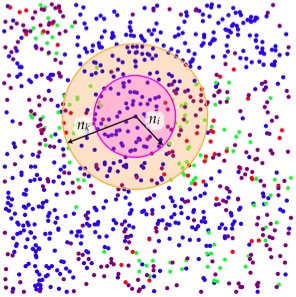
Each agent estimates the likelihood of their becoming infected if not vaccinated by observing the state of all other agents within a given distance nk. These others make up the agent’s knowledge neighborhood. From this observation the agent computes π = r + i, where r and i are the fraction of recovered and infected agents in the knowledge neighborhood. The only possibility of infection comes from other agents within a given distance ni of the new agent; these others make up an agent’s interaction neighborhood. In our model we specify the number of agents that should be in an interaction neighborhood on average, and choose ni accordingly.
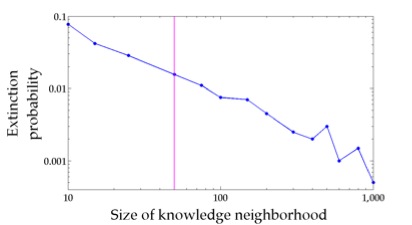
As illustrated in the figure below we find that when contagion dynamics are local and there is an intermediate relative cost r, the disease is less likely to be eradicated as agents have more information about their environment. In this simulation the interaction neighborhood was set to 50 (pink line) and the relative cost to 5.5. The extinction probability is calculated as the fraction of ensemble runs where the disease has been eradicated by time 150.
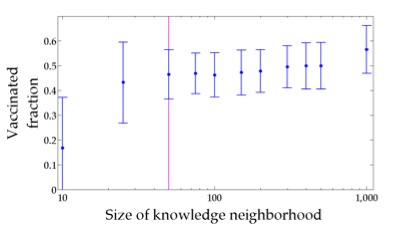
Below are the mean and standard deviation of the nonzero vaccination levels at time 150, as a function of the size of the information neighborhood. Vaccination levels increase with information, while at the same time standard deviation decreases, reflecting the fact that more information leads to dynamics determined by population averages rather than local neighborhoods. There is qualitatively different behavior in vaccination as we move from an information neighborhood smaller than the interaction neighborhood (pink line) to larger. To the left very low levels of infection and vaccination can survive in the population.
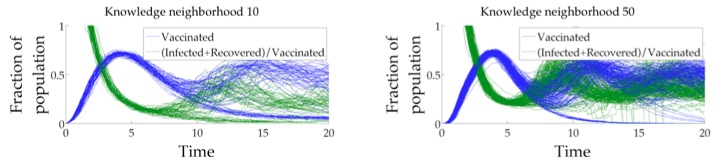
It may seem counterintuitive that when the information neighborhood is large average vaccination levels are highest and yet the disease is more likely to survive. However, on closer inspection this makes sense. In the time course below we can observe that vaccination levels have an oscillatory dynamic, but when the knowledge neighborhood is small (left panel) the fall in vaccination level is slower than when the knowledge neighborhood is large (right panel). Furthermore, although maximum and minimum nonzero vaccination levels are lower with smaller knowledge neighborhood, there is a lower average and minimum ratio of infected and recovered agents to vaccinated agents. That is, there are more vaccinated agents per infected or recovered individual on average, and vaccination in response to local but small infections can be sustained. This can be understood by noting that there is a threshold number of infected plus recovered neighbors above which an agent will vaccinate and below which it will not. The larger the knowledge neighborhood, the larger this threshold number is. Hence, agents can vaccinate when there are lower average infection levels (which could be high using a local measure) only when they observe less of the population. This turns out to be crucial in containing the infection.