Tour de Sys: The Traveler's View of a Network
Tomography is a procedure long used in the biological and physical sciences to study an object by producing images of many thin slices of it, rather than trying to study a picture of the entire object all at one. For example, the gross anatomy of organs is often illustrated using pictures of tissue slices taken at various depths, rather than trying to display a picture of the entire organ.A more general way to think about tomography is that it allows you to study a very complicated object by ignoring most of the information you have. Of course, this is done in a very structured way that depends on a well-defined parameter. In an organ tomogram, you may ignore all of the organ's anatomy except what you find at a height of 1 mm from the bottom. The height is a parameter; by varying the height, you view a series of extremely restricted pictures that, together, allow you to build up very detailed information about the organ, information that would not be available by looking at a three-dimensional picture of the organ's exterior. The idea of using a well-defined parameter to restrict and organize information is powerful, and we have been able to apply it to the study of networks in what we like to refer to as a novel way.
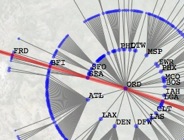
Any arbitrary graph can be transformed into a tree by choosing one vertex to serve as the root and including links only if they lie along the shortest path from the root to another vertex; such a tree is called the shortest-path tree rooted at the vertex. The shortest-path tree can be thought of as revealing that vertex's idea of the topology and statistical properties of the network. This tree is like one slice in an organ tomogram: it is a very restricted and simplified picture since the shortest-path tree will always have a regular structure, yet it still contains a great deal of information. Since every vertex has a different shortest-path tree, the number of different slices is the same as the number of vertices: the parameter of our tomography is the node index, or more intuitively the location in the network.
Using shortest-path trees to organize the network into a series of slices allows us to measure global properties of the system conditioned on location. The shortest-path tree of a node lays the network out into a set of rings: nodes that are one step away from the root, nodes that are two steps away, and so on. Very detailed information about one node's position in the network can be gleaned from the statistics of these rings, and from this a fuller characterization of a node appears. We have already used this procedure to identify a strong core-periphery structure in the US aviation network, and in the future we believe that this will lead to new methods of network attack and the ability to characterize the behavior of spreading processes on networks a priori.