Forecast and Control of Epidemics in a Globalized World
The application of mathematical modeling to the spread of epidemics has a long history and was initiated by Daniel Bernoulli’s work on the effect of cowpox inoculation on the spread of smallpox in 1760. Most studies concentrate on the local temporal development of diseases and epidemics. Their geographical spread is less well understood, although important progress has been achieved in a number of case studies. The key question, as well as difficulty, is how to include spatial effects and quantify the dispersal of individuals. Today’s volume, speed, and globalization of traffic, increasing international trade and intensified human mobility promote a complexity of human travel of unprecedented degree.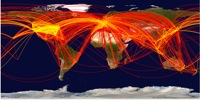
Figure 1: Nearly 95% of
the worldwide air transporation network. Lines
represent routes between connected airports, the
colorcode quantifies the number of passengers per day
along the routes.
The severe acute respiratory syndrome (SARS) which spread around the globe in a matter of months in 2003 has not only demonstrated that the geographic spread of modern epidemics vastly differs from historic ones but also the potential threat of emergent infectious diseases such as Hanta, West Nile and Marburg fever which can be contained to their endemic region only with increasing difficulty. Particularly in the light of an imminent H5N1 influenza A pandemic the knowledge of dynamical and statistical properties of human travel is of fundamental importance and acute.
In a this project we focused on the key mechanisms of the worldwide spread of modern infectious diseases. In particular we investigated to what extend the worldwide air transportation network plays a role in disseminating epidemics. To this end we compiled approximately 95% of the entire traffic network, which amounts to nearly 2 million flights per week between the 500 largest airports worldwide. Some of the questions we aimed to answer were: Is it possible to describe the worldwide spread of an epidemic based on a conceptionally lean model which incorporates the worldwide aviation network? If so, how reliable are forecasts put forth by the model? How important are fluctuations? What facilitates the spread? And, last but not least, what containment strategies and control measures can be devised as a result of computer simulations based on such a model?
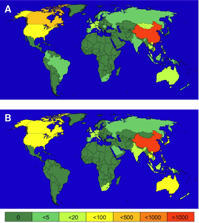
Figure 2:
(A) geographic spread of SARS in May
2003 as reported by the World Health Organization (WHO)
and the Center for Disease Control and Prevention
(CDC). The number of infecteds per country are encoded
by color. (B) The expected spread as
predicted by the model after a time of 90 days.
Depicted ist the expectation value of the number of
infecteds after 10000 simulations with an initial
outbreak in Hong Kong.
Our model consists of two parts: a local infection dynamics and the global traveling dynamics of individuals. The local dynamics is described by the SIR reaction kinetic scheme in which individuals are initially susceptible (S), become infected (I) and recover (R) from the disease, become immune and cannot be infected a second time.
Furthermore we assumed that the transport between urban areas is directly proportional to the traffic flux of passengers between them. Both constituents of our model are treated on a stochastic level, taking full account of fluctuations of disease transmission, latency, and recovery on the one hand and of the geographical dispersal of individuals on the other.
Fig. 2 depicts a comparison of the spread of SARS in May 2003 as reported by the World Health Organization and simulations of our model. Despite some differences the overall prediction of our model is surprisingly close to the observed global spread of SARS. The degree of agreement seems particularly surprising if one recalls the conceptual simplicity of our model and the fact that we incorporate fluctuations in the infection dynamics as well as the spatial dispersal.